Answer:
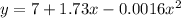
Parbolic path.
Explanation:
This is bidimensional motion, so the equation that relates the vertical and horizontal position is:
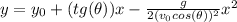
Here, v₀, θ y g are constants, then we can rewrite (1) as:
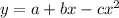
where:
Therefore the rectangular equation will be:
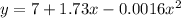
This type of path is a parabolic motion.
I hope it helps you!