(gof)(0) cannot be evaluated
Solution:
Given that,
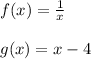
A composite function is denoted by (g o f) (x) = g (f(x)).
The notation g o f is read as “g of f”
Therefore, let us find whether (gof)(0) can be evaluated or not
To find (gof)(0):
(g o f) (x) = g (f(x))
Now substitute the given value of f(x)
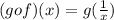
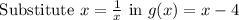

Now to find (gof)(0), substitute x = 0
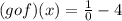
Since 1 divided by 0 is undefined, because any number divided by 0 is undefined
(gof)(0) cannot be evaluated