Question

F(x) = 1/x
g(x) = x - 4
Can you evaluate (gof)(0)? Explain why or why
not.

Answer 1

You must evaluate the function f first.

Division by 0 is undefined.

The composition cannot be evaluated.

Explanation:

Answer 2

(gof)(0) cannot be evaluated

Solution:

Given that,

`f(x) = (1)/(x)\\\\g(x) = x - 4`

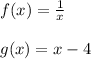
A composite function is denoted by (g o f) (x) = g (f(x)).

The notation g o f is read as “g of f”

Therefore, let us find whether (gof)(0) can be evaluated or not

To find (gof)(0):

(g o f) (x) = g (f(x))

Now substitute the given value of f(x)

`(g o f) (x) = g((1)/(x))`

`\text{ Substitute } x = (1)/(x) \text{ in } g(x) = x - 4`

`(g o f) (x) = (1)/(x) - 4`

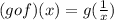
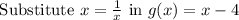
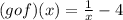
Now to find (gof)(0), substitute x = 0

`(g o f) (x) = (1)/(0) - 4`

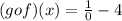
Since 1 divided by 0 is undefined, because any number divided by 0 is undefined

(gof)(0) cannot be evaluated