Question

A set of 15 different integers has a median of 25 and a range of 25. What is the greatest possible integer that could be in this set?A. 32

B. 37
C. 40
D. 43
E. 50

Answer 1

D. 43

Explanation:

We have been given that a set of 15 different integers has a median of 25 and a range of 25.

Since each data point is different, so we can represent our data points as:

`N_1,N_2,N_3,N_4,N_5,N_6,N_7,N_8, N_9,N_(10),N_(11),N_(12),N_(13),N_(14), N_(15)`

Since there are 15 data points, this means that median will be 8th data point.

We have been given that median is 25, so
`n_8=25`.

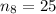Since each data point is different, so 7 data points less than 25 would be:

18, 19, 20, 21, 22, 23, 24.

We know that range is the difference between upper value and lower value.

`\text{Range}=\text{Upper value}-\text{Lower value}`

`\text{Range}+\text{Lower value}=\text{Upper value}`

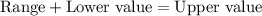
Upon substituting our given values, we will get:

`25+18=\text{Upper value}`

`43=\text{Upper value}`

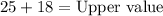
Therefore, the greatest possible integer in this set could be 43 and option D is the correct choice.

Answer 2

Option D.

Explanation:

It is given that a set of 15 different integers has a median of 25 and a range of 25.

Total number of integers is 15 which is an odd number.

`((n+1)/(2)) th=((15+1)/(2)) th=8th`

8th integers is median. It means 8th integers is 25.

7 different integers before 25 are 18, 19, 20, 21, 22, 23, 24.

It means the greatest possible minimum value is 18.

Range = Maximum - Minimum

25 = Maximum - 18

Add 18 on both sides.

25 +18 = Maximum

43 = Maximum

The greatest possible integer in the set is 43.

Therefore, the correct option is D.