Answer:
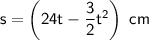
16 s
Explanation:
Given:
- s = s
- u = 0
- v = 48 - 3t
- a =
- t = t
Substituting values into SUVAT formula to find s in terms of t:
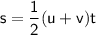
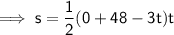
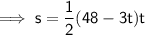
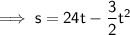
To find the time that elapses before the particle is back at A, set s to zero and solve for t:
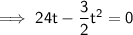
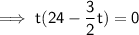

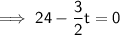

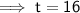
Therefore, t = 0 and t = 16, so the time that elapses before the particle is back again at A is 16 s