Question

A solid circular shaft and a tubular shaft, both with the same outer radius of c=co = 0.550 in , are being considered for a particular design. The tubular shaft has an inner radius of ci = 0.300 in The shafts are to be powered by a motor operating at a frequency of f = 2.70 Hz and are to handle an attached load. Assume the cross sections are uniform throughout the lengths of the shafts and that the materials have an allowable shear stress of τallow = 14.5 ksi .

Answer 1

The power for circular shaft is 7.315 hp and tubular shaft is 6.667 hp

Step-by-step explanation:

Polar moment of Inertia

`(I_p)s = \frac{\pi(0.55)4}2`

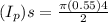
= 0.14374 in 4

Maximum sustainable torque on the solid circular shaft

`T_(max) = T_(allow) (I_p)/(r)`

=
`(14 * 10^3) * ((0.14374)/(0.55))`

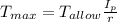
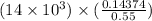
= 3658.836 lb.in

=
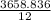`(3658.836)/(12)` lb.ft

= 304.9 lb.ft

Maximum sustainable torque on the tubular shaft

`T_(max) = T_(allow)( (Ip)/(r))`

=
`(14 *10^3) * ( (0.13101)/(0.55))`

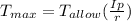
= 3334.8 lb.in

=
`((3334.8)/(12) )` lb.ft

= 277.9 lb.ft

Maximum sustainable power in the solid circular shaft

`P_(max) = 2 \pi f_T`

=
`2\pi(2.1) * 304.9`

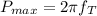
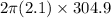
= 4023.061 lb. ft/s

=
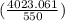`((4023.061)/(550))` hp

= 7.315 hp

Maximum sustainable power in the tubular shaft

`P _(max,t) = 2\pi f_T`

=
`2\pi(2.1) * 277.9`

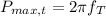
= 3666.804 lb.ft /s

=
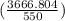`((3666.804)/(550))`hp

= 6.667 hp