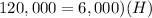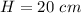Answer:
option D. 20 cm
Explanation:
step 1
Find the volume of the water
The volume of the water is equal to
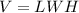
we have
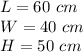
substitute
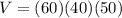
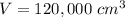 ---> volume of water
---> volume of water
step 2
Find the deep of the water, if the tank is returned to its horizontal position
we have
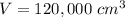
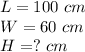
where
H is the deep of the water
substitute in the formula of volume
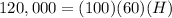
solve for H