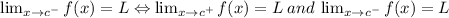Question

Does there exist a di↵erentiable function g : [0, 1] R such that g'(x) = f(x) for all x 2 [0, 1]? Justify your answer

Answer 1

No; Because g'(0) ≠ g'(1), i.e. 0≠2, then this function is not differentiable for g:[0,1]→R

Explanation:

Assuming: the function is
`f(x)=x^(2)` in [0,1]

And rewriting it for the sake of clarity:

Does there exist a differentiable function g : [0, 1] →R such that g'(x) = f(x) for all g(x)=x² ∈ [0, 1]? Justify your answer

1) A function is considered to be differentiable if, and only if both derivatives (right and left ones) do exist and have the same value. In this case, for the Domain [0,1]:

`g'(0)=g'(1)`

2) Examining it, the Domain for this set is smaller than the Real Set, since it is [0,1]

The limit to the left

`g(x)=x^(2)\\g'(x)=2x\\ g'(0)=2(0) \Rightarrow g'(0)=0`

`g(x)=x^(2)\\g'(x)=2x\\ g'(1)=2(1) \Rightarrow g'(1)=2`

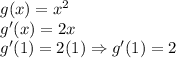
g'(x)=f(x) then g'(0)=f(0) and g'(1)=f(1)

3) Since g'(0) ≠ g'(1), i.e. 0≠2, then this function is not differentiable for g:[0,1]→R

Because this is the same as to calculate the limit from the left and right side, of g(x).

`f'(c)=\lim_(x\rightarrow c)\left [(f(b)-f(a))/(b-a) \right ]\\\\g'(0)=\lim_(x\rightarrow 0)\left [(g(b)-g(a))/(b-a) \right ]\\\\g'(1)=\lim_(x\rightarrow 1)\left [(g(b)-g(a))/(b-a) \right ]`

This is what the Bilateral Theorem says:

`\lim_(x\rightarrow c^(-))f(x)=L\Leftrightarrow \lim_(x\rightarrow c^(+))f(x)=L\:and\:\lim_(x\rightarrow c^(-))f(x)=L`