Answer:
AY = 10 cm.
Explanation:
Given that, ΔABC is similar to ΔAXY
and
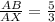
⇒
/(XY ) = (5)/(3)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/wnvgyib61qx2x5vr6j3w32az4kc6gl8vsc.png)
⇒ BC = XY× \frac{5}{3}[/tex] = \frac{20}{3}[/tex] (as XY = 4 cm given)
Now, check the attached figure,
given, BY bisects ∠XYC
let ∠XYB = ∠BYC = x
⇒ ∠AYX = 180-2x (angle on a straight line)
and also ∠AYX = ACB (similar triangle properties)
⇒ ∠ACB = 180-2x
Now, sum of angles in ΔBYC = 180°
⇒ ∠YBC = x
⇒ BC = YC (as two sides of equal angles are equal in a triangle)
⇒ YC = \frac{20}{3}[/tex]
And also
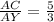
AC = AY + YC
⇒
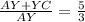
⇒
![\frac{AY+(20)/(3)]() }{AY } = \frac{5}{3}[/tex]
}{AY } = \frac{5}{3}[/tex]
⇒ 5AY = 3AY + 20
⇒ AY = 10 cm