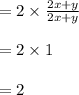Answer:
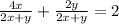
Explanation:
Given:
The expression to simplify is given as:
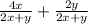
Since, the denominator is same, we add the numerators and divide it by the same denominator. This gives,
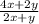
Now, we simplify further by factoring out the common terms from the numerator and denominator if possible.
We observe that, 2 is a common factor to both
 . So, we factor out 2 from the numerator. This gives,
. So, we factor out 2 from the numerator. This gives,
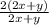
Now, the term
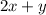 is common in both the numerator and denominator. Hence,
is common in both the numerator and denominator. Hence,
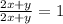
So, the simplified form is: