Answer:
 m/sec
m/sec
Step-by-step explanation:
According to the question
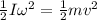
\omega= angular velocity = 14 spins per sec
I= MOI of the spinning eel= 0.5mR^2
m= mass of eel
v= linear velocity of eel.

solving for v in the above equation we get
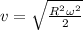
now \omega in radians = 14 rev/sec×2π radian/rev= 28π radian/sec
value of radius is not provided in the question
therefore we get
