Question

What's the formula for the standard error of the difference between the estimates of the population proportions, used in a confidence interval for the difference between two proportions?

Answer 1

`s_(p_1-p_2)=\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2) }`

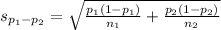
Explanation:

The formula for the standard error of the difference between the estimates od the population proportions is:

`s_(p_1-p_2)=\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2) }`

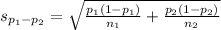
This is expected, as the variance of a sum (or a substraction) of two random variables is equal to the sum of the variance of the two variables.

Then, the standard error (or standard deviation) is the square root of this variance.