Option A
The equation
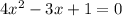 has two imaginary solutions
has two imaginary solutions
Solution:
Given that we have to determine the type and number of solutions of given quadratic equation
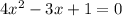
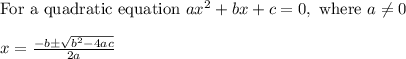
In a quadratic equation, the discriminant helps tell you the number of real solutions to a quadratic equation
In the case of a quadratic equation
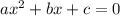 , the discriminant is
, the discriminant is


If
 , then the given quadratic equation has two imaginal roots which are complex conjugates
, then the given quadratic equation has two imaginal roots which are complex conjugates
Given quadratic equation is:
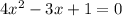
Here a = 4 and b = -3 and c = 1
The discriminant is given as:
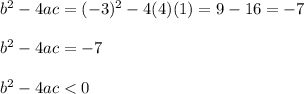
Therefore the given equation has two imaginary solutions