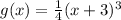Answer:
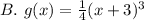
Explanation:
The misssing options are:
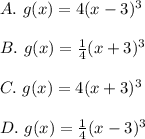
Some transformations for a function f(x) are shown below:
1. If
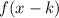 , the function is shifted right "k" units.
, the function is shifted right "k" units.
2. If
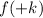 , the function is shifted left "k" units.
, the function is shifted left "k" units.
3. If
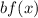 and
and
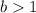 , the function is stretched vertically by a factor of "b".
, the function is stretched vertically by a factor of "b".
4. If
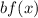 and
and
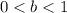 , the function is compressed vertically by a factor of "b".
, the function is compressed vertically by a factor of "b".
In this case, you know that the parent function f(x) is:

If the graph of the function g(x) is obtained by compressing vertically and shifting the function f(x) to the left, then:
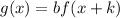 and
and
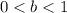
Based on this, you can identify that the following function could be the equation of the g(x):