Answer:
11 sections
Explanation:
This problem is called the circle cutting or pancake cutting problem.
Let the number of cuts or divisions by straight line = n
With this information it is possible to calculate any number of pieces or section a circle will be divided into what straight lines are drawn (cut) across the circle.
When a straight line is drawn across the circle, it divides the circle into 2 sections or regions. The nth straight lines will divide the circle into n new sections or regions, so the progression is;
f(1) = 2
f(2) = 2 + f(1)
f(3) = 3 + f(2)
.
.
.
f(n) = n + f(n-1)
Therefore,
f(n) = n + [(n-1) + f(n-2)}
= n + n-1 + ... + 2 + f(1)
= f(1) + ∑
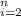 i
i
=
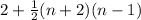
=
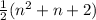
When n = 4
=
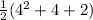
= 22/2
= 11 sections