Answer:
99% confidence interval is:
(0.00278 < P1 - P2< 0.15921)
Explanation:
For calculating a confidence intervale for the difference between the proportions of workers in the two cities, we calculate the following:

Where
 : proportion sample of individuals who worked
: proportion sample of individuals who worked
at more than one job in the city one
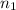 : Number of respondents in the city one
: Number of respondents in the city one
 : proportion sample of individuals who worked
: proportion sample of individuals who worked
at more than one job in the city two
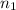 : Number of respondents in the city two
: Number of respondents in the city two
Then
α = 0.01 and α/2 = 0.005
and
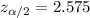
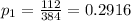
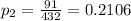
 and
and

The confidence interval is:
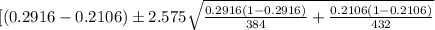
(0.00278 < P1 - P2< 0.15921)