Question

A car salesman had $65,100 in sales. He earned $1,953 in commission. What percent commission did he earn. Explain your answer.

How long was the loan

Interest earned = $299

Principal = $1300

Interest rate = 7%

Answer 1

1. The percent commission earned is 3%.

2. The loan period is 3.29 years.

Explanation:

1. Salesman has $65,100 in sales. He earned $1,953 in commission.

Let the percent commission earn be x%

Therefore, x% of the sales equals $1,953

`(x)/(100) of  $65,100 = $1,953`

`(x)/(100)  * 65100 = 1953\\(65100x)/(100) = 1953`

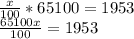
We cross multiply

`(65100x)/(100)  = 1953\\65100x = 1953 * 100\\65100x = 195300`

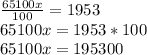
Divide both side by the coefficient of 'x' (65100)

`(65100x)/(65100) =  (195300)/(65100) \\x = 3`

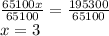
Therefore, the percent commission earned is 3%

2. Interest (I) = $299 Principal (P) = $1300 Rate (R) = 7%

The formula for finding interest is given as:
`I = (PRT)/(100)`

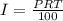
Therefore, substituting into the formula, we have:

`299 = (1300 * 7 * T)/(100)`

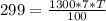
We are finding the time it takes the loan to earn an interest of $299

`299 = (1300 * 7 * T)/(100) \\299 = (9100T)/(100)`

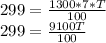
We cross-multiply:

`299 * 100 = 9100T\\29900 = 9100T`

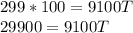
Divide both side by the coefficient of T (9100)

`(29900)/(9100)  = (9100T)/(9100)\\T = 3.29`

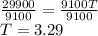
Therefore, the time taken for the loan to earn such interest is approximately 3.29 years