The solution for y in 2x − 5y ≤ 15 is
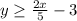
Solution:
Given that we have to find solution for given inequality for y
2x − 5y ≤ 15
Let us solve above equation for "y"
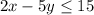
Add -2x on both sides
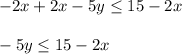
Divide by -5 on both sides
Remember that You can perform on operations on both sides of inequality, and have its truth value unchanged
But if we multiply or divide by a negative number, we must flip the sign
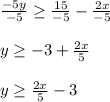
Thus solution for "y" is found