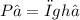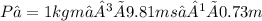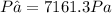Question

A garden hose with a small puncture is stretched horizontally along the ground. The hose is attached to an open water faucet at one end and a closed nozzle at the other end. As you might suspect, water pressure builds up and water squirts vertically out of the puncture to a height of 0.73 m. Determine the pressure inside the hose. (Enter your answer to the nearest 1000 Pa.) 7161.3 If you use the subscripts "1" and "2" respectively to represent a point in the hose before the leak and the site of the leak, how does h compare to h2? How does v1 compare to v2? What is the value of the pressure at the site of the puncture?

Answer 1

The pressure inside the hose 7000 Pa to the nearest 1000 Pa.

`h₁ = ((128μLQ)/(πD^(4) ) + ρgh₂)/(ρg)`

`V_(1) =V_(2)`

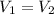
The pressure at the site of the puncture is
`P₂ =7161.3 Pa`

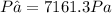
Step-by-step explanation:

According to Poiseuille's law,
`P_(1) - P_(2)  = (128μLQ)/(πD^(4) )`

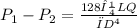
Where
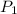`P_(1)` is the pressure at a point
`1` before the leak,
`P_(2)` is the pressure at the point of the leak
`2`, μ = dynamic viscosity, L = the distance between points
`1` and
`2`, Q = flow rate, D = the diameter of the garden hose.

Also, from the equation
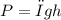`P =ρgh`, the equations
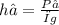`h₁ = \frac{P₁} {ρg}` and
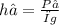`h₂ = \frac{P₂} {ρg}` can be derived.

Combining Poseuille's law with the above, we get
`<em>h₁ - ρgh₂ =  (128μLQ)/(πD^(4) )`

`h₁ = ((128μLQ)/(πD^(4) ) + ρgh₂)/(ρg)`

`V =(Q)/(A)`

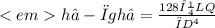
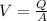
Since the hose has a uniform diameter, the nozzle at the end is closed and neither point
`1` nor
`2` lie after the puncture,

`V_(1) =V_(2)`

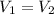
The pressure at the site of the puncture
`P₂ =ρgh₂`

`P₂ =1kgm⁻³ ×9.81ms⁻¹×0.73m`

`P₂ =7161.3 Pa`