Answer:
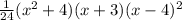
Explanation:
The zeroes are
2i,-3, and 4. So in factored form,
we have
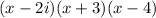
4 has a multiplicity of 2, so we have
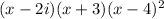
Rember that if 2i, is a zero, -2i, it's conjugate, is as well.
So we have
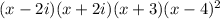
So let expand this out
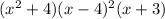
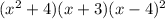
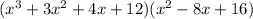
To avoid confusion, just look at the leading terms and the constant terms.
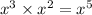
So this is a fifth degree polynomial.
However, if we plug in 0, we get
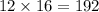
So how do we get this term to 8.
we divide the whole polynomial by 24.
or multiply it by 24
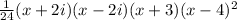
Here is the graph above:
The zeroes at 4, bounces off.
Their is a zero at -3,
and we have a y intercept of 8.