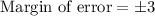Question

Determine the point estimate of the population mean and margin of error for the confidence interval.Lower bound is 22, upper bound is 28The point estimate of the population mean is ___The margin of error for the confidence interval is ___

Answer 1

1. The point estimate for population mean is 25.

2)

`\text{Margin of error} = \pm 3`

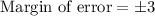
Explanation:

We are given the following information in the question:

Confidence interval: (22,28)

Confidence interval is calculated as:

`\text{Sample mean }\pm \text{ Margin of error}`

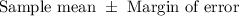
Thus, we can write the equations:

`\bar{x} - \text{Margin of error} = 22\\\bar{x} + \text{Margin of error} = 28`

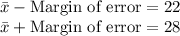
1) The point estimate of the population mean

To calculate the point estimate of the population mean we solve the two equations, to find the sample mean

Adding the two equations we get:

`2\bar{x} = 22+ 28 = 50\\\bar{x} = 25`

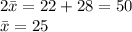
Thus, the point estimate for population mean is 25.

2) The margin of error for the confidence interval

Putting the values from the equation, we get:

`\text{Margin of error} = 28 - 25 = 3`

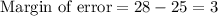
Thus, the margin of error f the given confidence interval is

`\text{Margin of error} = \pm 3`

Answer 2

Answer: The point estimate of the population mean is 25.

The margin of error for the confidence interval is 3 .

Explanation:

The confidence interval for population mean is given by :-

`(\overline{x}-E , \overline{x}+E)` , here
`\overline{x}` is the point estimate of the population mean and E is the margin of error .

As per given , we have

Lower bound of CI =
`\overline{x}-E =22` (1)

Upper bound of CI =
`\overline{x}+E =28` (2)

Add (1) and (2) , we get

`2\overline{x}=50\\\Rightarrow\ \overline{x}=25`

Subtract (1) from (2) , we get

`2E=6\\\Rightarrow\ E=3`

Hence, the point estimate of the population mean is 25.

The margin of error for the confidence interval is 3 .