Answer:
140
Explanation:
To construct a subset of S with said property, we have two choices, include 3 in the subset or include four in the subset. These events are mutually exclusive because 3 and 4 can not both be elements of the subset.
First, let's count the number of subsets that contain the element 3.
Any of such subsets has five elements, but since 3 is already an element, we only have to select four elements to complete it. The four elements must be different from 3 and 4 (3 cannot be selected twice and the condition does not allow to select 4), so there are eight elements to select from. The number of ways of doing this is
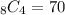 .
.
Now, let's count the number of subsets that contain the element 4.
4 is already an element thus we have to select other four elements . The four elements must be different from 3 and 4 (4 cannot be selected twice and the condition does not allow to select 3), so there are eight elements to select from, so this can be done in
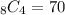 ways.
ways.
We conclude that there are 70+70=140 required subsets of S.