Question

What is the number of subsets of S= {1, 2, 3…10} that contain five element include 3 or 4 but not both?

Answer 1

140

Explanation:

To construct a subset of S with said property, we have two choices, include 3 in the subset or include four in the subset. These events are mutually exclusive because 3 and 4 can not both be elements of the subset.

First, let's count the number of subsets that contain the element 3.

Any of such subsets has five elements, but since 3 is already an element, we only have to select four elements to complete it. The four elements must be different from 3 and 4 (3 cannot be selected twice and the condition does not allow to select 4), so there are eight elements to select from. The number of ways of doing this is
`{}_8C_4=70`.

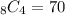Now, let's count the number of subsets that contain the element 4.

4 is already an element thus we have to select other four elements . The four elements must be different from 3 and 4 (4 cannot be selected twice and the condition does not allow to select 3), so there are eight elements to select from, so this can be done in
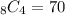`{}_8C_4=70` ways.

We conclude that there are 70+70=140 required subsets of S.