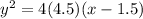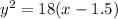Question

F(6,0), x= -3 use the formula to find the equation within given focus and directrix

Answer 1

`{y}^(2) = 18(x - 1.5)`

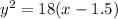
Explanation:

Step 1: Find the orientation of the conic.

The directrix is a vertical line so the conic section is sideways.

The conic section is a parabola in the form of

`{(y - k) {}^(2) } = 4p(x - h)`

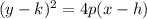
Where (h,k) is the vertex.

P is the distance from the vertex to focus. or the distance from the vertex to directrix.

This means the vertex lies halfway between the directrix and focus.

For conic section, the the y coordinate of the directrix must be the same for the y coordinate of the focus.

The directrix is (-3,0), which lines on the line x=-3

The focus is is (6,0) so halfway between them is 1.5.

So the vertex lies at

(1.5,0).

So h is 1.5, k is 0.

`{y}^(2) = 4p(x - 1.5)`

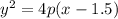
Now, let find p.

The distance from the focus to vertex is 4.5. Since the focus above the directrix, this distance is positive

So p=4.5

`{y}^(2) = 4(4.5)(x - 1.5)`

`{y}^(2) = 18(x - 1.5)`