Answer with Step-by-step explanation:
We are given that
COAL is a rhombus .
CA and LO are the diagonals of rhombus COAL.
CA=27 m
OL=19 m
We know that
Diagonals of rhombus are bisect to each other.
Let P(0,0) be the intersecting point of diagonals
Therefore, CP=PA
LP=PO
Length PO=
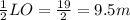
Length of CP=
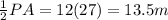
Let C(
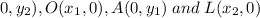 .
.
Distance formula:
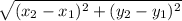
Using the formula
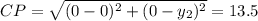
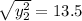
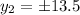
C(0,13.5) or (0,-13.5)
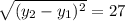
Substitute the value
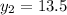
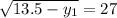
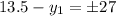
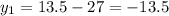
A(0,-13.5)
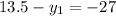

A(0,40.5)
Substitute
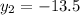
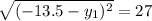
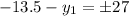
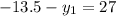

A(0,-40.5)
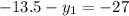
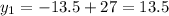
A(0,13.5)
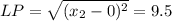
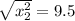
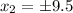
L(9.5,0) or L(-9.5,0)
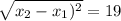
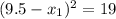
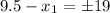
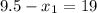
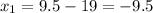
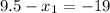
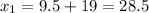
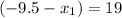
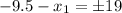
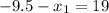
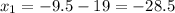
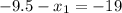
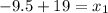

O(-9.5,0) or O(28.5,0) or (-28.5,0) or (9.5,0)