Answer:
Student needs pens= n = 27.04
Rounding off with upper floor function ⇒ n =28
Rounding off with lower floor function ⇒ n =27
Explanation:
Given that lifetime of each pen is a exponential random variable with mean 1 week.
Let
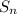 be total sum of lifetime of n pens.
be total sum of lifetime of n pens.
So mean of
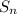 = μ = n.1
= μ = n.1
Standard deviation of
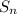 =
=
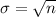
Probability that he doesnot run out of pens= 0.99
Considering Sn be sum of n lifetimes, using central limit theorem
![(S_(n)-n)/(√(n))\approx N(0,1)\\\\P(S_(n)>15)=[P((S_(n)-n)/(√(n)))>(15-n)/(√(n))]\\ 1-\phi((15-n)/(√(n)))=\phi(-((15-n)/(√(n))))=0.99\\](https://img.qammunity.org/2021/formulas/mathematics/college/w5nri2cyt16b26hp7dxvupe9n6rx75kx6f.png)
From table of standard normal distribution
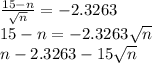
Solving the quadratic Equation in variable x we get
n=27.04