Question

A steel rotating-beam test specimen has an ultimate strength of 120 kpsi. Estimate the life of the specimen if it is tested at

a completely reversed stress amplitude of 70 kpsi.

Answer 1

104,576 cycles

Step-by-step explanation:

Step 1: identify given parameters

Ultimate strength of steel (
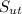`S_(ut)`)= 120 Kpsi

stress amplitude (
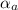`\alpha_(a)`)= 70 kpsi

life of the specimen (N) = ?

`N = ((\alpha_(a))/(a))^(1)/(b)`

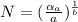
where a and b are coefficient of fatigue cycle

Step 2: calculate the the endurance limit of specimen

`S_(e) = 0.5*S_(ut)`

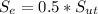
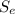`S_(e)` = 0.5*120 = 60 kpsi

Step 3: calculate coefficient 'a'

`a=\frac {(0.8XS_(ut))^2}{S_(e)}`

`a=\frac {(0.8X120)^2}{60}`

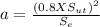
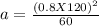
`a= 153.6 kpsi</p><p></p><p><u><strong>Step 4:</strong></u> calculate the coefficient 'b'</p><p>[tex]b =-(1)/(3)log((f*S_(ut) )/(S_(e)))`

`b =-(1)/(3)log((0.8*120)/(60))`

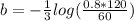
`b =-0.0680</p><p></p><p><u><strong>Step 5:</strong></u> calculate the life of the specimen</p><p>[tex]N=((\alpha_(a))/(a))^(1)/(b)`

`N=((70)/(153.6))^(1)/(-0.068)`

`N=104,576 cycles`

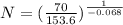
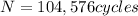
∴ the life (N) of the steel specimen is 104,576 cycles