Answer:
(b) a one-way between-subjects ANOVA
That's the correct option since we have one factor (class grade) and we have more than two groups.
Explanation:
(a) a two-independent sample t test
We can't apply a two independnet t test since we are comparing more than two groups (Freshman, sophomore, Junior and senior). And for this case when we have more than two groups, the most powerful method is the one way ANOVA between subjects.
(b) a one-way between-subjects ANOVA
That's the correct option since we have one factor (class grade) and we have more than two groups.
One way Analysis of variance (ANOVA) "is used to analyze the differences among group means in a sample".
The sum of squares "is the sum of the square of variation, where variation is defined as the spread between each individual value and the grand mean"
If we assume that we have
 groups and on each group from
groups and on each group from
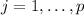 we have
we have
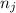 individuals on each group we can define the following formulas of variation:
individuals on each group we can define the following formulas of variation:
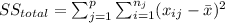
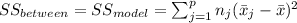
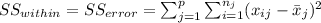
And we have this property

(c) a two-way between-subjects ANOVA
We can't apply a two way ANOVA since we have just one factor (or variable of interest) the class grades measured with a score. So then is not appropiate use this method for this case.
(d) both a two-independent sample t test and a one-way between-subjects ANOVA
False since we can't apply the two way ANOVA, that's not correct.