Question

At 35.0°C and 3.00 atm pressure, a gas has a volume of 1.40 L. What pressure does the gas have at 0.00°C and a volume of 0.950 L? Which equation should you use? A balloon containing 0.500 mol Ar at 0.00°C and 65.0 kPa pressure is expanded by adding more argon. How many moles of argon are added to bring the sample to a final volume of 60.0 L at 30.0°C and 45.0 kPa? What is the original volume of the gas? L

Answer 1

The final pressure of gas will be, 3.92 atm

The original volume of gas is, 17.46 L

The number of moles of argon gas added is, 0.57 mol.

Explanation :

Part 1 :

Combined gas law is the combination of Boyle's law, Charles's law and Gay-Lussac's law.

The combined gas equation is,

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

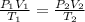
where,

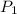`P_1` = initial pressure of gas = 3.00 atm

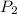`P_2` = final pressure of gas = ?

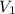`V_1` = initial volume of gas = 1.40 L

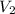`V_2` = final volume of gas = 0.950 L

`T_1` = initial temperature of gas =
`35.0^oC=273+35.0=308K`

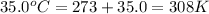
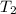`T_2` = final temperature of gas =
`0.00^oC=273+0.00=273K`

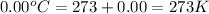
Now put all the given values in the above equation, we get:

`(3.00atm* 1.40L)/(308K)=(P_2* 0.950L)/(273K)`

`P_2=3.92atm`

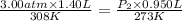
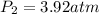
Therefore, the final pressure of gas will be, 3.92 atm

Part 2 :

First we have to calculate the original volume of gas.

Using ideal gas equation:

`PV=nRT`

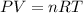
where,

P = pressure of gas = 65.0 kPa

V = volume of gas = 3.06 L

T = temperature of gas =
`0.00^oC=273+0.00=273K`

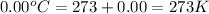
n = number of moles of gas = 0.500 mol

R = gas constant = 8.314 kPa.L/mol.K

Now put all the given values in the ideal gas equation, we get:

`(65.0kPa)* V=(0.500mol)* (8.314kPa.L/mol.K)* (273K)`

`V=17.46L`

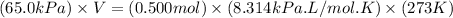
Now we have to calculate the final moles of sample of gas.

Using ideal gas equation:

`PV=nRT`

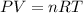
where,

P = pressure of gas = 45.0 kPa

V = volume of gas = 60.0 L

T = temperature of gas =
`30.0^oC=273+30.0=303K`

n = number of moles of gas = ?

R = gas constant = 8.314 kPa.L/mol.K

Now put all the given values in the ideal gas equation, we get:

`(45.0kPa)* (60.0L)=n* (8.314kPa.L/mol.K)* (303K)`

`n=1.07mol`

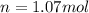
Now we have to calculate the number of moles of argon gas added.

Moles of argon gas added = Final moles of gas - Initial moles of gas

Moles of argon gas added = 1.07 mol - 0.500 mol

Moles of argon gas added = 0.57 mol

Thus, the number of moles of argon gas added is, 0.57 mol.