Answer
After inland population after migration allele frequency is 0.62 or 62%
Step-by-step explanation:
Given,
Coastal striped phenotype freq. = 0.22
ss = 0.22
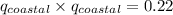
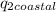 = 0.22
= 0.22
Similarly, inland striped phenotype freq. = 0.43
 = 0.43
= 0.43
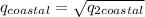
=
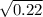
= 0.4690
 = 0.47 i.e. 47%
= 0.47 i.e. 47%
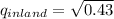
= 0.655
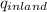 = 0.66 i.e. 66%
= 0.66 i.e. 66%
the migration range (m) is given as 20%
m= 0.2
allele freq. after migration = pre migration + ∆q
here,
∆q = change in the allele frequency
or
migration of allele freq. from coastal to inland
=
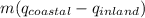
= 0.2 (0.47 – 0.66)
=
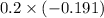
= - 0.0382
∆q = -0.04 i.e. 4%