Answer:
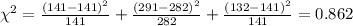

And we can find the p value using the following excel code:
"=1-CHISQ.DIST(0.861,2,TRUE)"
Since the p value is higher than the significance level
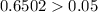 we FAIL to reject the null hypothesis at 5% of significance, and we can conclude that we don't have significant differences for the proportions assumed.
we FAIL to reject the null hypothesis at 5% of significance, and we can conclude that we don't have significant differences for the proportions assumed.
Explanation:
Previous concepts
A chi-square goodness of fit test "determines if a sample data matches a population".
A chi-square test for independence "compares two variables in a contingency table to see if they are related. In a more general sense, it tests to see whether distributions of categorical variables differ from each another".
Solution to the problem
Assume the following dataset:
White = 141, Pink = 291, Red= 132
We need to conduct a chi square test in order to check the following hypothesis:
H0: There is no difference with the proportions assumed
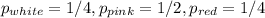
H1: There is difference with the proportions assumed
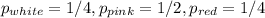
The level of significance assumed for this case is

The statistic to check the hypothesis is given by:
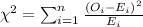
The table given represent the observed values, we just need to calculate the expected values with the following formula
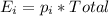
And the calculations are given by:

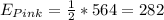

And now we can calculate the statistic:
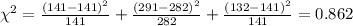
Now we can calculate the degrees of freedom for the statistic given by:
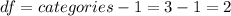
And we can calculate the p value given by:

And we can find the p value using the following excel code:
"=1-CHISQ.DIST(0.861,2,TRUE)"
Since the p value is higher than the significance level
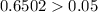 we FAIL to reject the null hypothesis at 5% of significance, and we can conclude that we don't have significant differences for the proportions assumed.
we FAIL to reject the null hypothesis at 5% of significance, and we can conclude that we don't have significant differences for the proportions assumed.