Question

Triangles Q R S and X Y Z are shown. Angles Q S R and X Z Y are right angles. Angles Q R S and X Y Z are congruent. The length of Y Z is 9, the length of X Z is 12, and the length of hypotenuse X Y is 15. Given △QRS ~ △XYZ, what is the value of tan(Q)? Three-fifths Three-fourths Four-fifths Four-thirds

Answer 1

Three-fourths

Explanation:

see the attached figure to better understand the problem

we know that

∠QSR≅∠XZY ---> given problem

∠QRS≅∠XYZ ---> given problem

so

△QRS ~ △XYZ ----> by AA Similarity theorem

Remember that, if two triangles are similar, then the ratio of its corresponding sides is proportional and its corresponding angles are congruent

That means

`(QS)/(XZ)=(QR)/(XY)=(RS)/(YZ)`

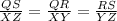
∠Q≅∠X

∠R≅∠Y

∠S≅∠Z

In the right triangle XYZ

Find the tangent of angle X

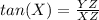`tan(X)=(YZ)/(XZ)` ---> opposite side angle X divided by adjacent side angle X

substitute the given values

`tan(X)=(9)/(12)`

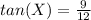
Simplify

`tan(X)=(3)/(4)`

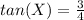
Remember that

∠Q≅∠X

so

`tan(Q)=tan(X)`

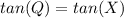
therefore

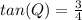`tan(Q)=(3)/(4)` ---->Three-fourths