Answer:
a) The Net power developed in this air-standard Brayton cycle is 43.8MW
b) The rate of heat addition in the combustor is 84.2MW
c) The thermal efficiency of the cycle is 52%
Step-by-step explanation:
To solve this cycle we need to determinate the enthalpy of each work point of it. If we consider the cycle starts in 1, the air is compressed until 2, is heated until 3 and go throw the turbine until 4.
Considering this:
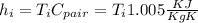


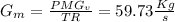
Now we can calculate the enthalpy of each work point:
h₁=281.4KJ/Kg
h₂=695.41KJ/Kg
h₃=2105KJ/Kg
h₄=957.14KJ/Kg
The net power developed:
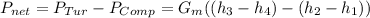
The rate of heat:
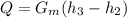
The thermal efficiency:
