Question

After the mill in a small town closed down in 1970, the population of that town started decreasing according to the law of exponential growth and decay. By 1990, the population had decreased to 143 thousand. By 2019, the population further decreased down to 98 thousand. Heat was the original population in 1970.

Answer 1

`P_o = (143000)/(e^(-20*0.01303024661))=110193.69`

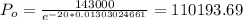
And we can round this to the nearest up integer and we got 110194.

Explanation:

The natural growth and decay model is given by:

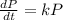`(dP)/(dt)=kP` (1)

Where P represent the population and t the time in years since 1970.

If we integrate both sides from equation (1) we got:

`\int (dP)/(P) =\int kdt`

`ln|P| =kt +c`

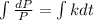
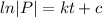
And if we apply exponentials on both sides we got:

`P= e^(kt) e^k`

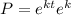
And we can assume
`e^k = P_o`

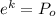
And we have this model:

`P(t) = P_o e^(kt)`

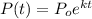
And for this case we want to find
`P_o`

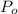
By 1990 we have t=20 years since 1970 and we have this equation:

`143000 = P_o e^(20k)`

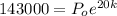
And we can solve for
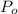`P_o` like this:

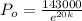`P_o = (143000)/(e^(20k))` (1)

By 2019 we have 49 years since 1970 the equation is given by:

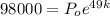`98000 = P_o e^(49k)` (2)

And replacing
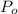`P_o` from equation (1) we got:

`98000=(143000)/(e^(20k)) e^(49k) =143000 e^(29k)`

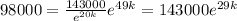
We can divide both sides by 143000 we got:

`(98000)/(143000) =0.685 = e^(29k)`

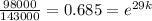
And if we apply ln on both sides we got:

`ln(0.685) = 29k`

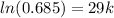
And then k =-0.01303024661[/tex]

And replacing into equation (1) we got:

`P_o = (143000)/(e^(-20*0.01303024661))=110193.69`

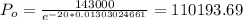
And we can round this to the nearest up integer and we got 110194.