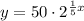Find the solution of the differential equation dy/dt = ky, k a constant, that satisfies the given conditions. y(0) = 50, y(5) = 100 - QAmmunity.org

Find the solution of the differential equation dy/dt = ky, k a constant, that satisfies the given conditions. y(0) = 50, y(5) = 100

asked May 13, 2021 171k views

2 Answers

Answer:

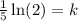
$(1)/(5)\ln(2)=k$

Solution without isolating
:

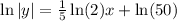
$\ln|y|=(1)/(5)\ln(2)x+\ln(50)$

Solution with isolating
:

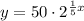
$y=50 \cdot 2^{(1)/(5)x}$

Step-by-step explanation:

(dy)/(dx)=ky

We will separate the variables so we can integrate both sides.

Multiply
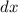on both sides:

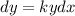
dy=ky dx

Divide both sides by
:

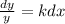
(dy)/(y)=k dx

Now we may integrate both sides:

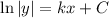
$\ln|y|=kx+C$

The first condition says
y(0)=50 .

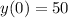Using this into our equation gives us:

$\ln|50|=k(0)+C$

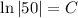
$\ln|50|=C$

So now our equation is:

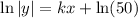
$\ln|y|=kx+\ln(50)$

The second condition says
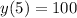y(5)=100 .

Using this into our equation gives us:

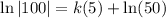
$\ln|100|=k(5)+\ln(50)$

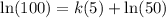
$\ln(100)=k(5)+\ln(50)$

Let's find
.

Subtract
$\ln(50)$ on both sides:

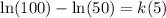
$\ln(100)-\ln(50)=k(5)$

I'm going to rewrite the left hand side using quotient rule for logarithms:

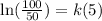
$\ln((100)/(50))=k(5)$

Reducing fraction:

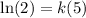
$\ln(2)=k(5)$

Divide both sides by 5:

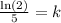
$(\ln(2))/(5)=k$

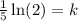
$(1)/(5)\ln(2)=k$

So the solution to the differential equation satisfying the give conditions is:

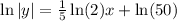
$\ln|y|=(1)/(5)\ln(2)x+\ln(50)$

Most likely they will prefer the equation where
is isolated.

Let's write our equation in equivalent logarithm form:

$y=e^{(1)/(5)\ln(2)x+\ln(50)}$

We could rewrite this a bit more.

By power rule for logarithms:

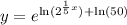
$y=e^{\ln(2^{(1)/(5)x})+\ln(50)}$

By product rule for logarithms:

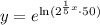
$y=e^{\ln(2^{(1)/(5)x} \cdot 50)}$

Since the natual logarithm and given exponential function are inverses:

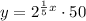
$y=2^{(1)/(5)x} \cdot 50$

By commutative property of multiplication:

$y=50 \cdot 2^{(1)/(5)x}$

Rajeev Varshney answered May 16, 2021

by Rajeev Varshney

6.7k points

Search QAmmunity.org