Answer:
Reject at 5%, accept at 1% the null hypothesis
Explanation:
Set up hypotheses as

(Left tailed test)
Population std dev = 6
Sample std error =
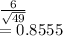
Mean difference = -1.5
Since sigma is known we can use Z test
Z = mean diff/std error = -1.7533
p value = 0.039
a) Since p value <0.05 we reject H0. There is evidence that the true mean is different from 60 wpm
b) Yes, because his sample would have been biased since he may want to prove his belief so slow or inefficient persons he would have selected in the sample.
c) For 99% confidence interval critical value = 2.58
Confidence interval for population mean = 58.5±2.58*std error
=(56.2928, 60.7072)
Since this contains 60, the hypothesized mean, we accept null hypothesis.
we do not have evidence to reject the claim that the average graduate can type 60 wpm at 1% level of significance.