Question

An automobile dealer wants to see if there is a relationship between monthly sales and the interest rate. A random sample of 4 months was taken. The results of the sample are presented below. Monthly Sales (Y) Interest Rate (In Percent) (X) 22 9.2 20 7.6 10 10.4 45 5.3 a) Use the method of least squares to compute an estimated regression line. b) Obtain a measure of how well the estimated regression line fits the data.

Answer 1

a)
`y=-6.254 x +75.064`

b) r =-0.932

The % of variation is given by the determination coefficient given by
`r^2` and on this case
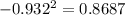`-0.932^2 =0.8687`, so then the % of variation explained by the linear model is 86.87%.

Explanation:

Assuming the following dataset:

Monthly Sales (Y) Interest Rate (X)

22 9.2

20 7.6

10 10.4

45 5.3

Part a

And we want a linear model on this way y=mx+b, where m represent the slope and b the intercept. In order to find the slope we have this formula:

`m=(S_(xy))/(S_(xx))`

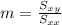
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

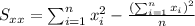
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=278.65-(32.5^2)/(4)=14.5875`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i){n}}=696.9-(32.5*97)/(4)=-91.225`

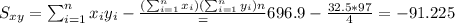
And the slope would be:

`m=(-91.225)/(14.5875)=-6.254`

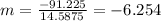
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(32.5)/(4)=8.125`

`\bar y= (\sum y_i)/(n)=(97)/(4)=24.25`

And we can find the intercept using this:

`b=\bar y -m \bar x=24.25-(-6.254*8.125)=75.064`

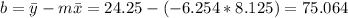
So the line would be given by:

`y=-6.254 x +75.064`

Part b

For this case we need to calculate the correlation coefficient given by:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

`r=(4(696.9)-(32.5)(97))/(√([4(278.65) -(32.5)^2][4(3009) -(97)^2]))=-0.937`

So then the correlation coefficient would be r =-0.932

The % of variation is given by the determination coefficient given by
`r^2` and on this case
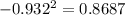`-0.932^2 =0.8687`, so then the % of variation explained by the linear model is 86.87%.