Answer:
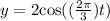
Explanation:
We have been given that an object oscillates 4 feet from its minimum height to its maximum height. The object is back at the maximum height every 3 seconds. We are asked to find the cosine function that can be used to model the height of the object.
We know that standard form of cosine function is
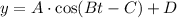 , where,
, where,
|A| = Amplitude,
Period =
 ,
,
C = Phase shift,
D = Vertical shift.
Since distance between maximum and minimum is 4, therefore, amplitude will be half of it, that is,
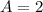 .
.
Since objects gets back to its maximum value in every 3 seconds, therefore, period of the function is 3 seconds. We know that period is given by
 , therefore, we can write
, therefore, we can write
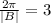 , therefore,
, therefore,
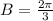 .
.
We haven't been given any information about phase and mid-line, we can assume the values of C and D to be zero .
Therefore, our function required function would be
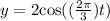 .
.