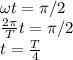Answer:
t = T/4
Step-by-step explanation:
The power delivered to the mass by the spring is work done by the spring per second.
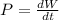
The work done by the spring is equal to the elastic potential energy stored in the spring.
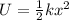
The maximum energy stored in the spring is at the amplitude of the oscillation.
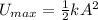
So the first time the mass reaches to its amplitude can be found by the following equation of motion:
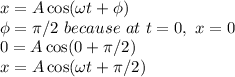
When the mass reaches the amplitude:
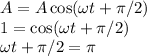
because cos(π) = 1.
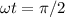
Using ω = 2π/T,