Question

At a steam power plant, steam engines work in pairs, the heat output of the first one being the approximate heat input of the second. The operating temperatures of the first are 750◦C and 440◦C respectively, and of the second 415◦C and 270◦C.

Answer 1

The rate at which coal burned is 111.12 kg/s.

Step-by-step explanation:

Given that,

First initial temperature =750°C

First final temperature =440°C

Second initial temperature =415°C

Second final temperature =270°C

Suppose If the heat of combustion of coal is
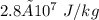`2.8×10^(7)\ J/kg`, at what rate must coal be burned if the plant is to put out 950 MW of power? Assume the efficiency of the engines is 65% of the Carnot efficiency.

The work done by first engine is

`W=eQ`

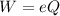
The work done by second engine is

`W'=e'Q'`

`W'=e'Q(1-e)`

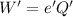
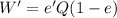
Total out put of the plant is given by

`W+W'=950\ MW`

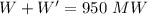
Put the value into the formula

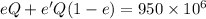`eQ+e'Q(1-e)=950*10^(6)`....(I)

We need to calculate the efficiency of first engine

Using formula of efficiency

`e=65%(1-(T_(L))/(T_(H)))`

`e=0.65(1-(440+273)/(750+273))`

`e=0.196`

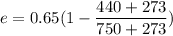
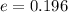
We need to calculate the efficiency of second engine

Using formula of efficiency

`e'=65%(1-(T_(L))/(T_(H)))`

`e'=0.65(1-(270+273)/(415+273))`

`e'=0.136`

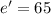
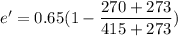
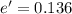
Put the value of efficiency for first and second engine in the equation (I)

`Q(0.196+0.136(1-0.196))=950*10^(6)`

`Q=(950*10^(6))/((0.196+0.136(1-0.196)))`

`Q=3111.24*10^(6)\ W`

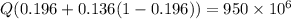
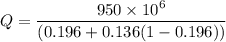
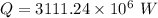
We need to calculate the rate at which coal burned

Using formula of rate

`R=(Q)/(H_(coal))`

`R=(3111.24*10^(6))/(2.8×10^(7))`

`R=111.12\ kg/s`

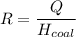
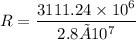
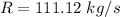
Hence, The rate at which coal burned is 111.12 kg/s.