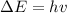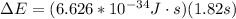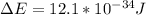Question

For small amplitudes of oscillation the motion of a pendulum is simple harmonic. Consider a pendulum with a period of 0.550 s Find the ground-level energy. Express your result in joules Find the ground-level energy. Express your result in election volts

Answer 1

To solve this problem we will use the concepts related to the expression of energy for harmonic oscillator. From our given values we have that the period is equivalent to

`T = 0.55s`

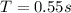
Therefore the frequency will be the inverse of the period and would be given as

`f= (1)/(T)`

`f = (1)/(0.55)`

`f = 1.82s^(-1)`

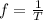
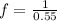
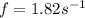
The ground state energy of the pendulum is,

`E = (1)/(2) hv`

`E = (1)/(2)(6.626*10^(-34)J\cdot s)(1.82s^(-1))`

`E = 6.03*10^(-34)J`

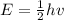
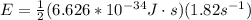
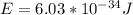
The ground state energy in eV,

`E = 6.03 * 10^(-34)J((1eV)/(1.6*10^(-19)J))`

`E = 3.8*10^(-15)eV`

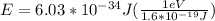
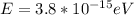
The energy difference between adjacent energy levels,

`\Delta E = hv`

`\Delta E = (6.626*10^(-34)J\cdot s)(1.82s)`

`\Delta E = 12.1*10^(-34)J`