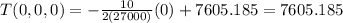Answer:
a)
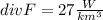
b)
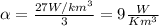
c)
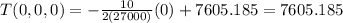
Explanation:
(a) Suppose that the actual heat generation is 27W/km3 What is the value of div F? div F- Include units)
For this case the value for div F correspond to the generation of heat.
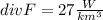
(b) Assume the heat flows outward symmetrically. Verify that
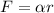 where
where
 . Find a α, (Include units.)
. Find a α, (Include units.)
For this case we can satisfy this condition:
![div[\alpha (xi +yj +z k)]]=\alpha(1+1+1)=3\alpha](https://img.qammunity.org/2021/formulas/mathematics/college/56r4ixwg9dfp6lxp1y2wkghz733j1c4t9f.png)
And since we have the value for the
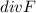 we can find the value of
we can find the value of
 like this:
like this:
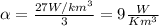
(c) Let T (x,y,z) denote the temperature inside the earth. Heat flows according to the equation F= -k grad T where k is a constant. If T is in °C then k=27000 C/km. Assuming the earth is a sphere with radius 6400 km and surface temperature 20°C, what is the temperature at the center? 27,0 C/km.
For this case we have this:
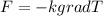
And grad T represent the direction of the greatest decrease related to the temperature.
So we have this equation:
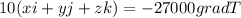
And we can solve for grad T like this:
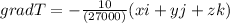
Andif we integrate in order so remove the gradient on both sides we got:
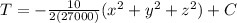
For our case we have the following condition:
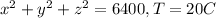
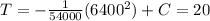
And we can solve for C like this:
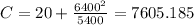
So then our equation would be given by:
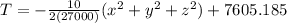
And for our case at the center we have that
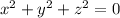
And we got: