Question

If y=sin(x-sinx), what is the smallest positive value of x for which the tangent line is parallel to the x-axis

(a) 1.677

(b) 2.310

(c) 3.142

(d) 3.973

(e) 6.283

Answer 1

Option b ) 2.310

Explanation:

Given that the function is

`y = sin (x-sinx)`

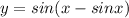
For finding when the tangent is parallel to x axis, we must find the least positive value of x for which y' i.e. derivative =0

Differentiate y with respect to x using chain rule.

`y' = cos(x-sinx) * (1-cosx)`

Equate this to 0

Either one factor should be zero.

`cos(x-sinx)=0\\x-sinx =(\pi)/(2) \\`

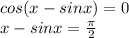
x=2.31 satisfies this

For the other root,

`1-cos x =0\\cos x =1\\x =0\\`

Since positive least value is asked we can say

x =2.310

Option b