Question

Change to slope-intercept form. Then find the y-intercept, first point, and second point.

-x+3y>6


(choices in photo)

Answer 1

1)
`y> (x)/(3)+2` 2) (0,2) 3) The first and second Points must have x coordinate <-6, or y-coordinate y >2 e.g. (-7,2), (-6,3)

Explanation:

1) To Rewrite it as Slope-intercept form, is to isolate the y on the left side and on the right side the rest of the inequality.

`-x+3y>6\Rightarrow 3y>x+6 \Rightarrow y> (x+6)/(3)\Rightarrow y> (x)/(3)+2`

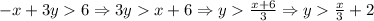
2) Since this is a linear inequality the y intercept is given by "b" parameter.
`y> mx+b \Rightarrow y> (x)/(3)+2 \Rightarrow b=2`

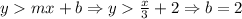
So the y-intercept is y > 2, coordinate point (0,2). In the graph, we have a dashed line over 2.

3) Since there no choices, the points that satisfy this inequality lie within the green area. We know that the points for this inequality must satisfy x < -6 or y> 2:

Testing for (-7,2) for x<-6 ⇒-7 <-6

`-x+3*y>6\\-(-7)+3*2>6\\7+6>6\\13>6\:\\True\\`

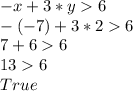
Testing for (-6,3) for y>2 ⇒3>2

`-x+3*y>6\\-(-6)+3*3>6\\6+9>6\\15>6\:True\\`