Question

Find the sample size, n, needed to estimate the percentage of adults who have consulted fortune tellers. Use a 0.02 margin of error, use a confidence level of 98% and use results from a prior poll suggesting that 20% of adults have consulted fortune tellers.

Answer 1

Answer: 2172

Explanation:

Formula to find the sample size n , if the prior estimate of the population proportion(p) is known:

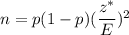`n= p(1-p)((z^*)/(E))^2` , where E= margin of error and z* = Critical z-value.

Let p be the population proportion of adults have consulted fortune tellers.

As per given , we have

p= 0.20

E= 0.02

From z-table , the z-value corresponding to 98% confidence interval = z*=2.33

Then, the required sample size will be :

`n= 0.20(1-0.20)((2.33)/(0.02))^2`

`n= 0.20(0.80)(116.5)^2`

`n= 2171.56\approx2172`

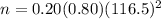
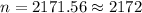
Hence, the required sample size = 2172