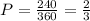Question

In a plane, points P and Q are 20 inches apart. If point R is randomly chosen from all the points in the plane that are 20 inches from P, what is the probability that R is closer to P than it is to Q?

Answer 1

`P = (2)/(3)`

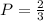
Explanation:

All the points in the plane that are 20 inches from P constituing a circle with center in P and with radius 20 inch

We need find the angle in this circle by which the point R is closer to P than it is to Q. The limit situation occurs when the distances from P to R and from R to Q are equals and have the value 20 inches. In this situation the points P, R y Q form a equilater triangle with angles of value 60°.

Thus, the point R is closer to P than it is to Q in 240° of the circle, except 60° above of the line PQ and 60° below the line PQ.

Then the probability is

`P= (240)/(360) = (2)/(3)`