Answer:
Check it down.
Explanation:
Injective functions or One to one functions are functions in each one element of A set is is mapped to another element of B set
1) Let's start by listing supposition and their respective Reasons
Suppose:
 is injective then
is injective then
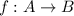 is also injective.
is also injective.
Reason: Given
2) Since we are dealing with injective (one to one) functions, we can rightly proceed:
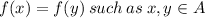
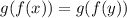
Given the fact that


Then we can say that since
 f: A is an injective too ("one to one" ) function.
f: A is an injective too ("one to one" ) function.