Question

Which of the following circular rods, (given radius r and length l) each made of the same material and whose ends are maintained at the same temperature will conduct most heat?

a) r = 2r₀; l = 2l₀
b) r = 2r₀; l = l₀
c) r = r₀; l = 2l₀
d) r = r₀; l = l₀

Answer 1

Step-by-step explanation:

Heat flow in a circular rod is given by

`Q=(kAdT)/(dx)`

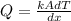
where Q= heat flow

k=thermal conductivity

A=area of cross-section

dT=Change in temperature

dx=change in length

Also A can be written as

`A=\pi r^2`

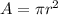
thus Q is Proportional to

`Q\propto (r^2)/(l)`

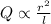
For option (a)

`Q\propto ((2r_0)^2)/(2l_0)`

`Q\propto (2r_0^2)/(l_0^2)`

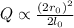
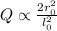
(b)
`Q\propto ((2r_0)^2)/(l_0)`

`Q\propto (4r_0^2)/(l_0)`

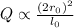
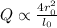
(c)
`Q\propto (r_0^2)/(2l_0)`

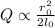
(d)
`Q\propto (r_0^2)/(l_0)`

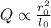
So Rod b will conduct the most Heat