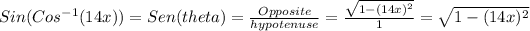Answer:
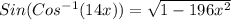
Step-by-step explandation:
First of all, from the figure we can define the cosine and sine functions as
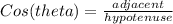
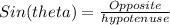
And by analogy with the statement:
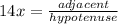
Which can be rewritten as:
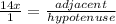
You have then that, for the given triangle, the values of the adjacent and hypotenuse sides, are then given by:
:
Adjacent=14x
Hypotenuse=1
And according to the Pythagorean theorem:
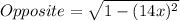
Finally, by doing:
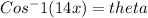
We have that: