Question

Find an equation of the slant asymptote. Do not sketch the curve. y = 5x4 + x2 + x x3 − x2 + 5

Answer 1

The slant asymptote is
`y=5 x + 5`.

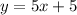Explanation:

Line
`y=mx+b` is a slant asymptote of the function
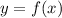`y=f{\left(x \right)}`, if either
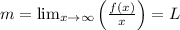`m=\lim_(x \to \infty)\left(\frac{f{\left(x \right)}}{x}\right)=L` or
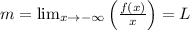`m=\lim_(x \to -\infty)\left(\frac{f{\left(x \right)}}{x}\right)=L`, and L is finite.

We want to find the slant asymptotes of the function

`f(x)=(5 x^(4) + x^(2) + x)/(x^(3) - x^(2) + 5)`

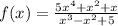
First, do polynomial long division

`(5 x^(4) + x^(2) + x)/(x^(3) - x^(2) + 5)=5 x + 5+(6 x^(2) - 24 x - 25)/(x^(3) - x^(2) + 5)`

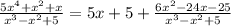
Next, we use the above definition,

The first limit is

`\lim_(x \to \infty)\left((6x^2-24x-25)/(x^3-x^2+5)\right)=0`

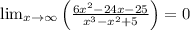
The second limit is

`\lim_(x \to -\infty)\left((6x^2-24x-25)/(x^3-x^2+5)\right)=0`

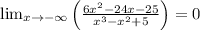
The rational term approaches 0 as the variable approaches infinity.

Thus, the slant asymptote is
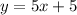`y=5 x + 5`.